Doing more makes you faster - II

Last time, we saw how doing a single extra instruction made our code 3 times faster.

But less code in a loop should surely always be faster… right?

Consider these two pieces of code doing binary exponentiation:

Here is the vimdiff between the 2 snippets of code

Clearly, we are doing much more work in the code on the right. When x & 1 == 0, we unnecessarily perform the operation (ans * 1) & MOD, also the extra instruction arr[1] = a might also be taking up some extra ops…

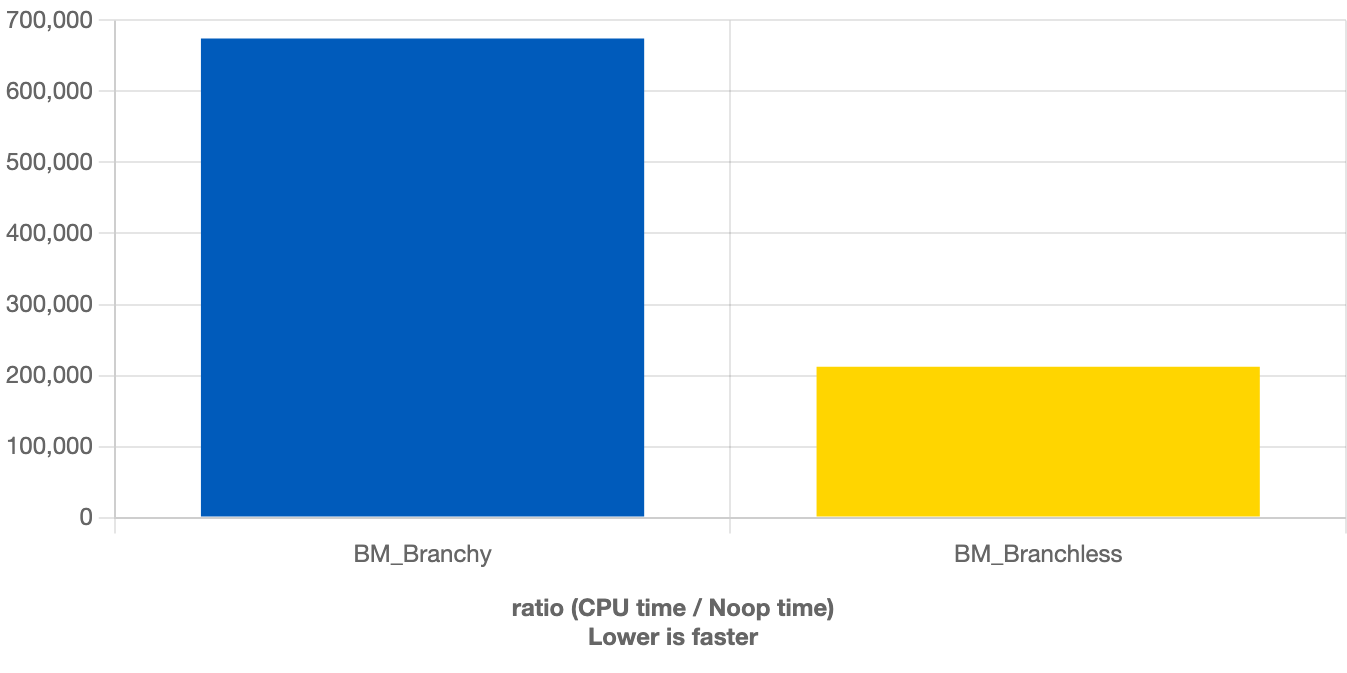
So the code on the left should be a clear winner. Let us benchmark just to be sure.

Branchless computing, makes us 3.2 times faster!

But why is that so?

Branches suck! The villain here is the if. Those bits of x look random to the CPU, so every time the branch predictor guesses wrong, the pipeline flushes and you lose dozens of cycles.

In the branchless version, the CPU no longer needs to guess. The work is perfectly predictable, even if it’s a bit redundant. The CPU stays busy, the pipeline stays full - and the code flies.

Let’s do double the work everywhere and make our code 3.2 times faster, and get bonuses 3.2 times larger this time, right?

Well, not quite yet. keen-eyed among you would have noticed that we are performing the operation & MOD instead of % MOD. That’s because MOD is chosen to be of the form 2^n - 1.

If we replace the & operator with the % operator, we’re just 1.1× faster.
So, as always, we have to benchmark - because in some cases, we might even become slower. Further, our results also depend on the randomness of the exponent.

If you’d like to dive deeper into how branch predictors work, I highly recommend Prof. Smruti Ranjan Sarangi’s Advanced Computer Architecture book. His accompanying course is also an absolute goldmine. I was lucky to study under him

More uses

This kind of optimisation is more useful than you might think .It not only prevents the branch predictor from working against us but can also help keep our instruction and data caches warm.

For a classic case of use in HFTs, consider a code snippet like

if(can_cancel){
  order->cancel();
}

Most likely, we will not be cancelling the order, so the branch predictor takes the “not-taken” route. But when we do want to cancel the order, each cycle matters.

So instead, we have a couple of approaches.

Similar to the one above, we can have an array of orders: the one at index 0 is a dummy order, and the one at index 1 is the actual order.

std::array<Order,2> orders = {dummy, order};
orders[can_cancel]->cancel();

Another approach is to take that decision of cancelling the order as late as possible:

order->cancel(isDummy=!can_cancel)

So every time we execute the cancel function, we try to execute as much of it as possible. When we actually have to cancel - and when it matters the most - we’ll already be executing that code path.

This approach keeps our instruction cache and data caches warm, and also ensures the branch predictor doesn’t get in our way.

Thank you!¹

1. I originally saw this optimization discussed in a CppCon talk but couldn’t find the exact video later. Please share a link in the comments, if you happen to find it. ↩